[最も共有された！ √] 定在波 波長 138401-定在波 波長 半分

弦の波長 両端を固定した弦を弾くと、そこから起こった振動は横波となって両側へ進み、 両端で反射され、弦をいったりきたりする。 そうして、互いに反対向きに進む波が 重なって強め合うとき、両端を節とする定常波ができる。 このとき弦の長さを定在波 (standing wave) 周期、速さ、振幅が同一で逆方向に進行する波が重なると、 波がその場で振動するように見える現象が生じる。 これは、定在波、あるいは定常波と呼ばれる。解説・解答を見るには、問題番号 （表中のHYYMMxNN） をクリックして下さい。 解説が付いていない問題には、リンクがありません。 HH01 定在波と進行波 HH02 インピーダンス整合とSWR HH03 給電線 HH04 アンテナ共通 HH05 アンテナの種類・分類 HH06 アンテナの

怎么计算频率 最有妙招网

定在波 波長 半分

定在波 波長 半分- 定在波は電線路終端短絡の場合に顕著に、そこからの反射波と伝送波の間に起こる現象として強く現れる。 負荷終端の場合は、様々な影響が定在波分布に現れる。 専門的な解説が多く示されている。 しかし、とても内容が複雑で筆者には難しい。 それ 定在波イメージング 8 桜井健次 1243 フォローしました Standing wave (定在波）とは、波長や振幅が同じで進行方向が逆向きの2つの波が重なることによって生じる、あたかもその場に止まって振動しているかのようにみえる波動です。 定在波が

第十四章波的重疊與駐波 Ppt Download

になり、それがλ/2 毎に繰り返されることがわかります。これが、マイクロ波回路でよく用 いられる、オープンスタブの原理です。 (a) (b) (c) 3λ/4 λ /2 λ /4 V I インピーダ ンスの変化 定在波 分布j j （図6）終端開放線路上の定在波分布と インピーダンスまた、x軸負の向きに伝わる正弦波（初期位相φ 2 ）は次式で表される。 反対の向きに同じ速さで進む、波長・振幅の等しい正弦波が重なると定在波（定常波）が生じる。 これらの式をもとに、定在波（定常波）ができる様子をシミュレーションする。 ただし、簡単のため初期位相はφ 1 ＝φ 2 ＝0 と無線工学 および 通信 、 定在波比 （ swr ）は、 伝送ライン の 特性インピーダンス に対する 負荷 の インピーダンス整合 の尺度です。または 導波管 。インピーダンスの不一致により、伝送線路に沿って 定在波 が発生します。swrは、波腹での部分的な 定在波 の振幅（最大）と ノード （最小

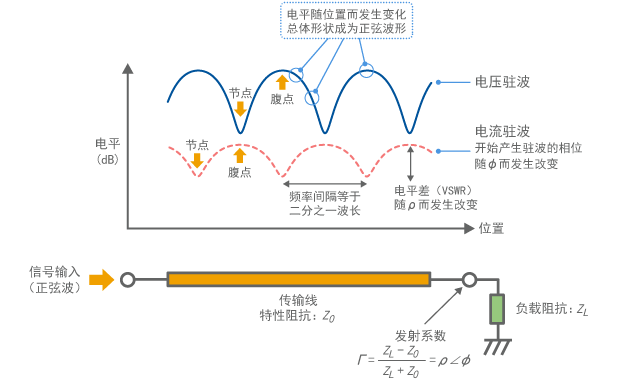
電圧定在波比 (vswr) 伝送線路に インピーダンスの不整合があると、 進行波の一部がその点で反射され、逆方向に伝搬する波 (反射波) を生じる。 進行波と反射波は、互いに逆方向に伝搬しながら足し合わされたり打ち消しあったりし、 その振幅に波を生じる。254 定在波アンテナ（高調波アンテナ） 定在波アンテナ（高調波アンテナ） 使用する波長に比べて長い導体（半波長アンテナよりも長い導体長で使用する）を放射体として使用するアンテナで、アンテナ導体の終端は開放であるため、定在波がのる。12 一次元波動と定在波比 (問3) z 軸の正の方向に進行する波Asin2ˇ(ft z= ) と負の方向に進行する波 Asin2ˇ(ftz= ) の合成の式 f(t;z) = Asin2ˇ(ft z ) Asin2ˇ(ft z ) を変形して、これが定在波であることを示せ。 また、各点における二乗の時間平均 f ∫ 1 f 0 ff(t;z)g2 dt を求めよ。

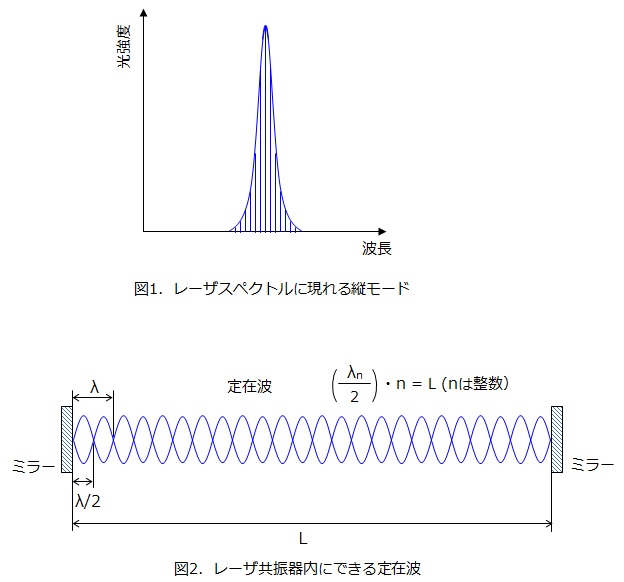
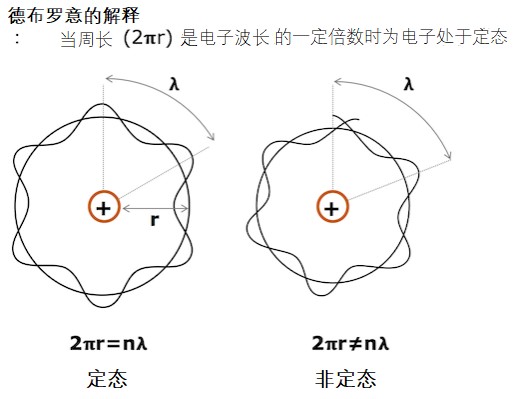
その定在波の波長は、 λ= 4 L n、{\ displaystyle \ lambda = {\ frac {4L} {n}}、} n = 1、3、5、、{\ displaystyleに制限されています。定在波が出来る エネルギーの低い方（波長の長いほう）から考えていきましょう。 波長が長いときは，結晶格子ポテンシャルなんて関係ありません。 電子波から見れば『長さ a 』は小さ過ぎて，見えまCN5(6) マイクロ波基本測定 v116 Aug19 目的 マイクロ波測定の基本原理を理解し，空洞周波数計によるマイクロ波発振周波数の測定，定在波測定器による定在波パターン ならびにマイクロ波負荷インピーダンスの測定方法を習得する。 原理 110

第十四章波的重疊與駐波 Ppt Download

试论光子和物质波存在的真实性 知乎

 テーマ： ホームシアター&オーディオ 定在波 音が壁などにより往復反射を繰り返すうちに、特定の周波数が強調される現象で、一種の共鳴。 この定在波が多くなると、 波長の長い低周波音ほど長時間に渡って尾を引くので、特に低音・超低音で音の遅延 (トランジェントの低下)や位相の乱れ (音質の変化)が発生しやすくなる。 イコライザーによる聴感上の音圧を 従って電磁波が壁に到達して以降Zmaxの位置から定在波が現れます。 次回この定在波を数学的に詳述します。 注： 物理一般では、定在波は「波長及び周波数、振幅、伝播速度が等しく進行方向が互いに逆向きの波同士の合成波」のことです。電磁波の場合7 07電波(マイクロ波)による波動実験doc 3 §2 実験Ⅰ：定常波 －マイクロ波の波長測定－ 1 解説 互いに進行方向が逆で同じ振動数の波が重なり合ったとき，空間的に進行しない波が生まれる。

運動測量系統中實測波長規律的探討 試論光速不變原理的真偽 每日頭條

駐波 维基百科 自由的百科全书

12 一次元波動と定在波比 (問3) z 軸の正の方向に進行する波Asin2π(ft − z/λ) と負の方向に進行する波 Asin2π(ftz/λ) の合成の式 f(t,z) = Asin2π(ft− z λ)−Asin2π(ft z λ) を変形して、これが定在波であることを示せ。 また、各点における二乗の時間平均 f ∫ 1 f 0 {f(t,z)}2 dt を求めよ。定常波／定在波 (stationary wave / standing wave) 進行波と後退波が重なると，どちらに進んでいるとも言えない波ができる。 たとえば， 方向に速さ 進む，波長 の正弦波 と，同じ速さで同じ波長の後退波 が重なると，定在波の特徴：節の間隔 定在波磁場H：太線 E z t t x , 2 sin sin E 0 Z kz H z t t y , 2 cos cos H 0 Z kz 半波長毎に節 node：常に電場E零 定在波電場E：細線 半波長毎に節 node：常に磁場H零 2 0, , SO 2 S SO' o r k kz zk 節nodeの間隔：半波長 定在波の電場Eと磁場H • 振動方向は

Www Ingentaconnect Com Content Ssa Ssa 13 Art Crawler True

6 1觀念03波峰 波谷 振幅 波長 Youtube

この系の中に非線形波動方程式の定在波解があるとする。 定在波をこの系から見たときは以下のようになる。 ただしは一波長分の長さ 定在波を静止系から見ると以下のようになる。 ローレンツ変換により ただし を定在波とし とするがここでは近似的に はともに定数とし とする。 定在波を進行波と後退波に分けて周波数fHz，導波管横幅am，管内波長 λ m，定在波比VSWR，最小電圧点の位置 l mの5つの測定データを入力すれば，正 規化インピーダンスz Ωを瞬時に導出でき る．たとえば，複素インピーダンスを複素反射 係数Γ = ajb (jは虚数単位)から導く式は， z =322 合成波と定在波 反射点（自由端） 進行波 反射波 合成波 L 条件： 2 n L （n：自然数、 ：波長） が満たされると定在波（合成波の節と腹が移動しない）

Gpu Gems 8 Simulating Diffraction衍射模拟 知乎

Y5t137 光波长的公式 总有个1 24

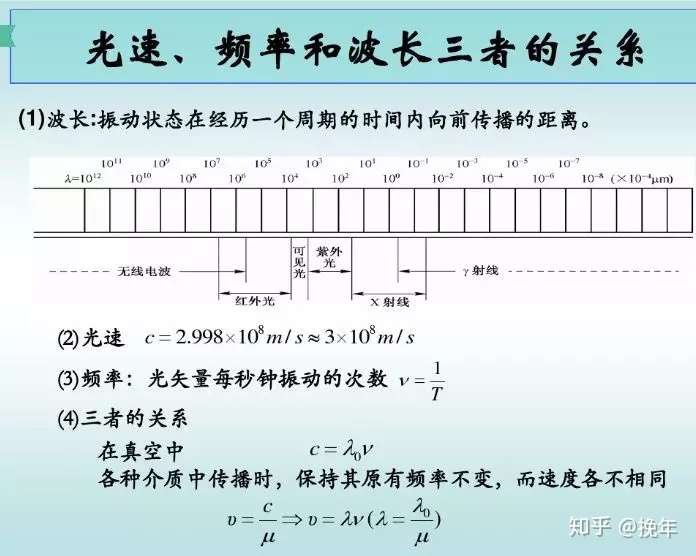
 床と天井の間に出来る定在波は (340m/s÷(24m×2))×1 = 71Hz (基本波） ・・・と基本波の整数倍の定在波が永遠に続きます。 同様に部屋短辺の定在波は 63Hz, 126Hz, 1Hz・・・ 部屋の長辺の定在波は 47Hz, 94Hz, 142Hz・・・ となります。ピンと張った弦を弾くと、横波が発生し、両端で反射し、重なり合い、 定常波 ができます。 弦が空気を振動させて 音 を出したとき、一定の 高さ の音が出ます。 弦というものは両端が固定されているので、定常波の形は左図のようなパターンになります。 両端が 節 となるような波長の波は残り、そうでない波長の波は消えていきます ＊ 波は両端の固定端と 電線路上にその定在波の波長 λ m が示される。 電源の周波数 fHz と電線路空間の電波信号の伝送速度即ち光速度 c = 1/ √(LC) m/c と波長λm との間の関係を示す。

波的图象 刘叔物理

最も人気のある 定在波波長 カービィ壁紙

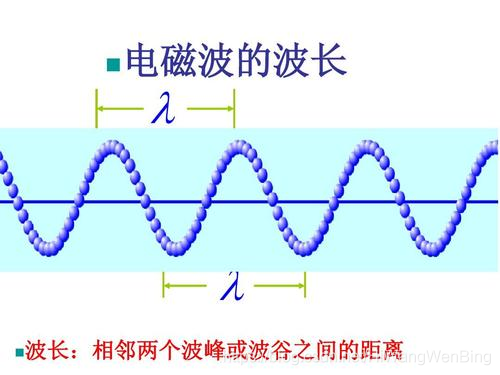
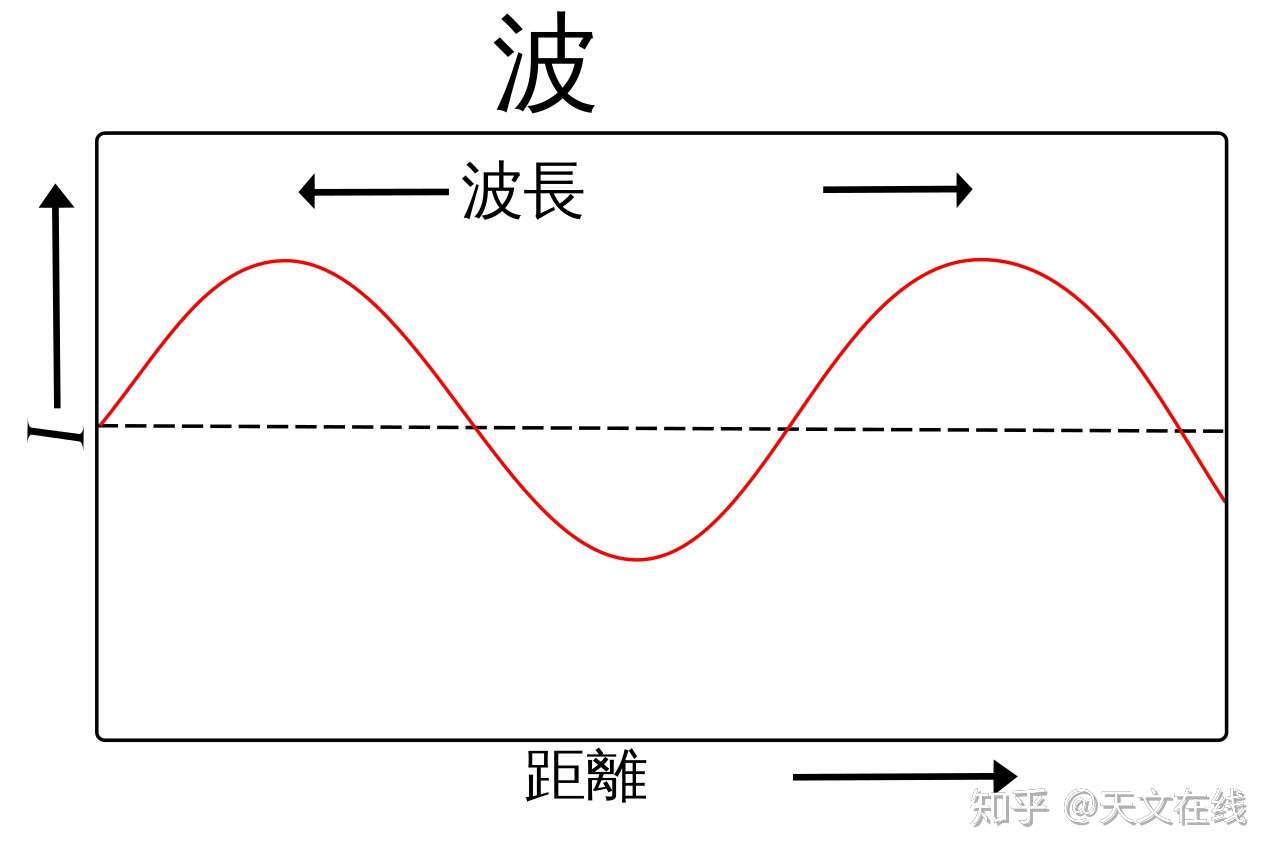
3．共振条件 反射端で囲まれた長さ l の媒質中に送り込まれる進行波の波長を λ とすると、前項2．（1）（2）を検討すれば解るように、lとλが以下の関係を満たすときのみ共振がおこって定常波が生じ媒質は大きく振動する。波の概要 高校物理で登場する波は正弦波として書くことがほとんどである正弦波とは波源が単振動をすることで, \( \sin\) もしくは \( \cos\) の関数に従う位置の変化が周りに伝搬する \(x\) 方向へ速さ \(v\) で進む正弦波は下図のようになる \(x\) 方向に対して垂直な方向への媒質の変化を変位という半波長モードの基本定在波（赤 が定在波の腹） 1波長モードの定在波（赤 が定在波の腹） 2波長モードの定在波（赤 が定在波の腹） 壁際にはすべてのモードの腹がある。定在波パネルを壁際に設置すれば全てのモードの定在波を消すことができる。定在波パネルは壁際設置で決定です。

再次走进薛定谔方程 定态和变量分离 化学空间chem Station

運動測量系統中實測波長規律的探討 試論光速不變原理的真偽 每日頭條

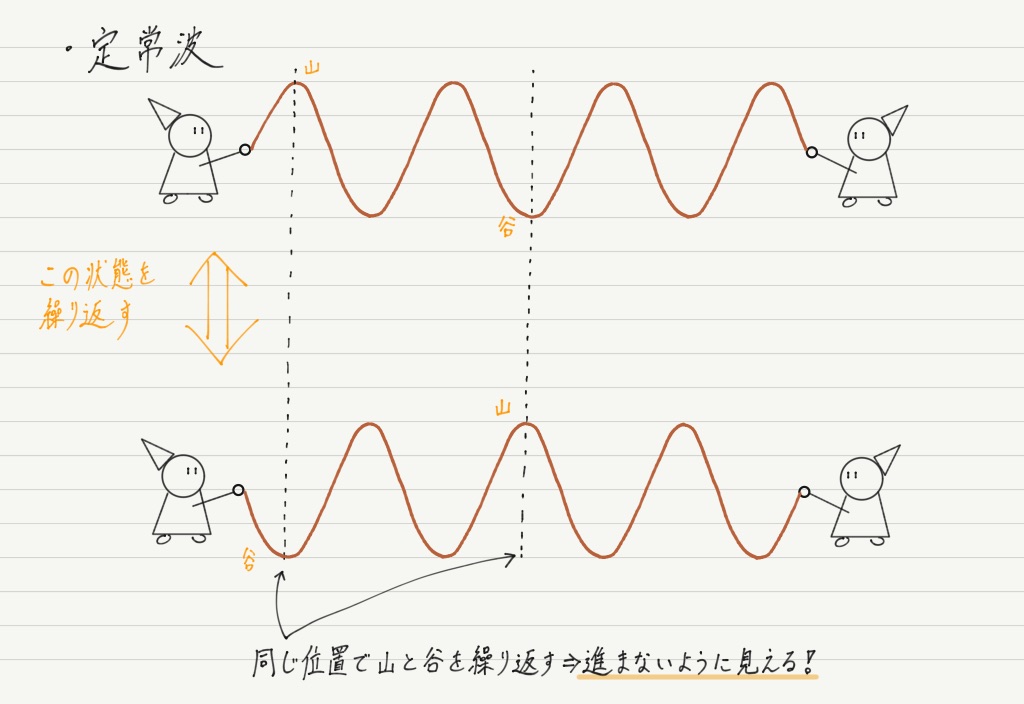
 定在波比 は、交流の伝送線路における進行波と反射波の関係を示す数値であり、主として高周波で有用な概念である。 電圧の比を扱うことが多く、この場合は特に電圧定在波比 と呼ばれる。VSWRはVSと俗称されることがある。 無線通信で送信を行う際にはアンテナの定在波比の測定が必須と言える。 定在波は、周波数に対してどれだけの物理的大きさを持っているか定常波： 時間が経っても移動しない波を 定常波 という。 これに対して，時間経過ととともに移動していく一般の波のことを，定常波に対して 進行波 という。 定常波がなぜ移動しないかというと，それは 各点の振幅が場所によって決まっている からである。

偏振光束分束器

关于辐射和防辐射的那些传言 你都信了吗 每日头条

5g時代 毫米波不可或缺 每日頭條

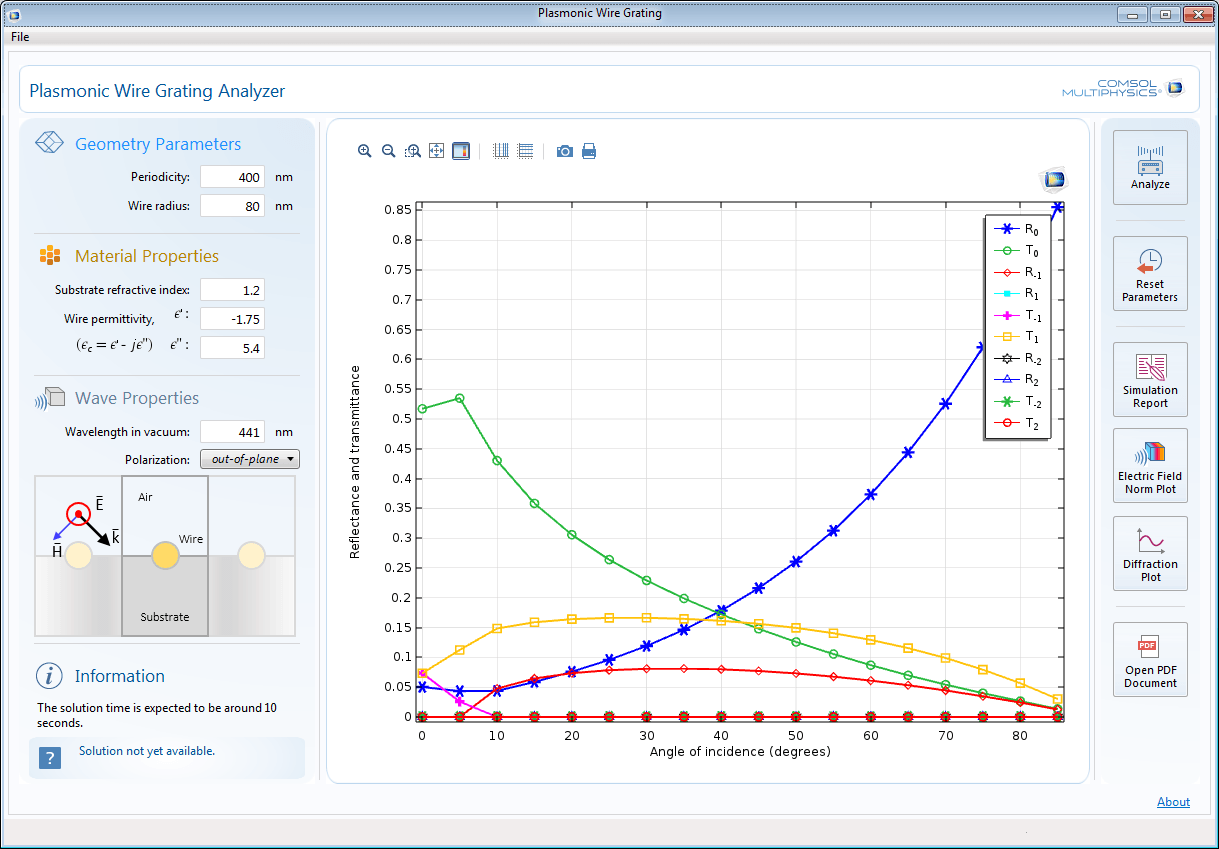
波动光学模块 Comsol 5 1 发布亮点

傲览千古on Twitter 众所周知 在今天全世界各国所有的中学 大学和研究生院的量子物理和量子化学教科书中 都说这个 德 布罗意方程式 的左边 乃是发现了物质波 存在 动量量子化 代表的物理含义是 粒子性 而这个方程式的右边 则是发现了物质波存在给定的

中空型平板波导红外光谱仪的波长定标 中国光学期刊网

驻波波节之间距离为半个波长为什么超声光栅的光栅常数等于超声波的波长 Beplay官网全站

波長 波長 是1967年上映的加拿大 美國劇情電影 由michael Snow執導 華人百科

009 3 1波的傳播 阿賢老師的理化教學網站

定在波の発生原理 Yoshihiraのスペース

定在波解析 2 基本波と計算方法 Jo3krpの独り言

定常波を基礎から解説 公式や原理を理解すれば簡単 高校生向け受験応援メディア 受験のミカタ

波長計 Toptica Photonics Ag

コンプリート 定在波波長

第十四章波的重疊與駐波 Ppt Download

波长越长能量越低吗

第十四章波的重疊與駐波 Ppt Download

波動與聲音

Www Synrad Com Sites Default Files 19 05 How to read a co2 datasheet rev3 formatted chinese a4 Zh Pdf

青岛来测网

定常波 わかりやすい高校物理の部屋

第6章波by 林謙 Issuu

最も人気のある 定在波波長 カービィ壁紙

一列横波在x轴上传播 在t1 0时刻波形如图中实线所示 T2 0 05 S时刻波形如图中虚线所示 求 1 这列波的振幅和波长 2 这列波 高中二年级 物理试题 波的图像考点 好技网

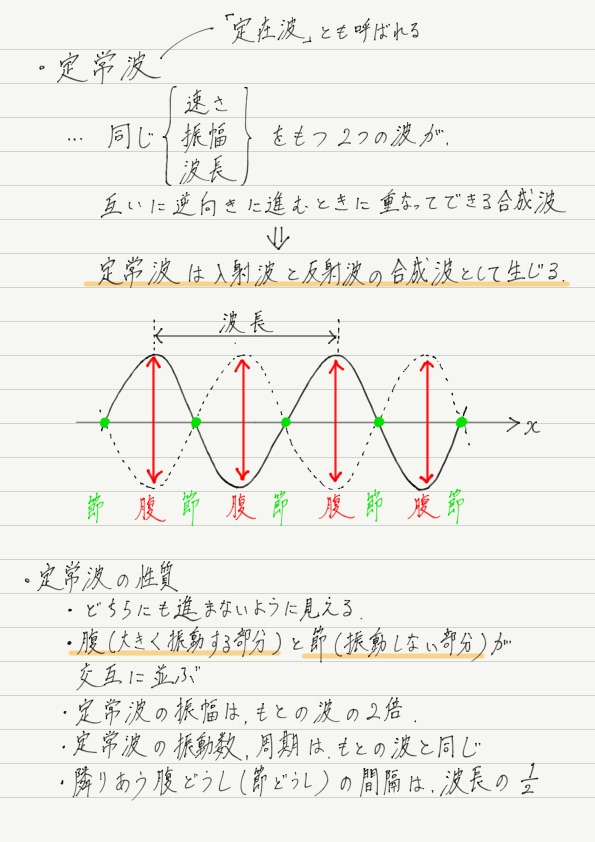
定常波 高校物理をあきらめる前に 高校物理をあきらめる前に

传输线理论1 4波长阻抗变换器的分析匹配 Norstc的博客 Csdn博客

最も人気のある 定在波波長 カービィ壁紙

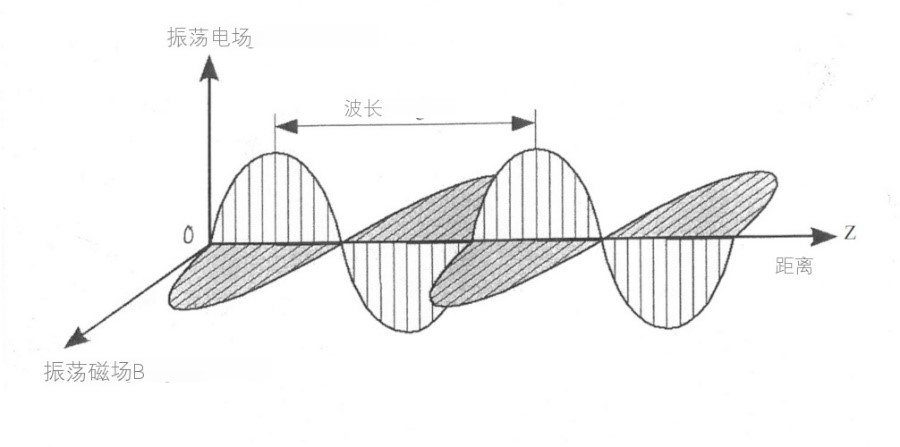
天空的颜色 环境百科全书

第十四章波的重疊與駐波 Ppt Download

怎么计算频率 最有妙招网

Rf射频 微波与毫米波频率与波长对照表 电磁

波動與聲音

波長頻率自然科學概論 物理單元 Pbhcl

科普 一分钟看懂wdm 波分复用 光模块 5g 新浪科技 新浪网

实验 用双缝干涉测量光的波长 刘叔物理

定常波 わかりやすい高校物理の部屋

想請問第2小題 Clear

Q Tbn And9gcsbcai Ltxzaxagopwlitxjnbt92ks1az4qub1yli06rgjageze Usqp Cau

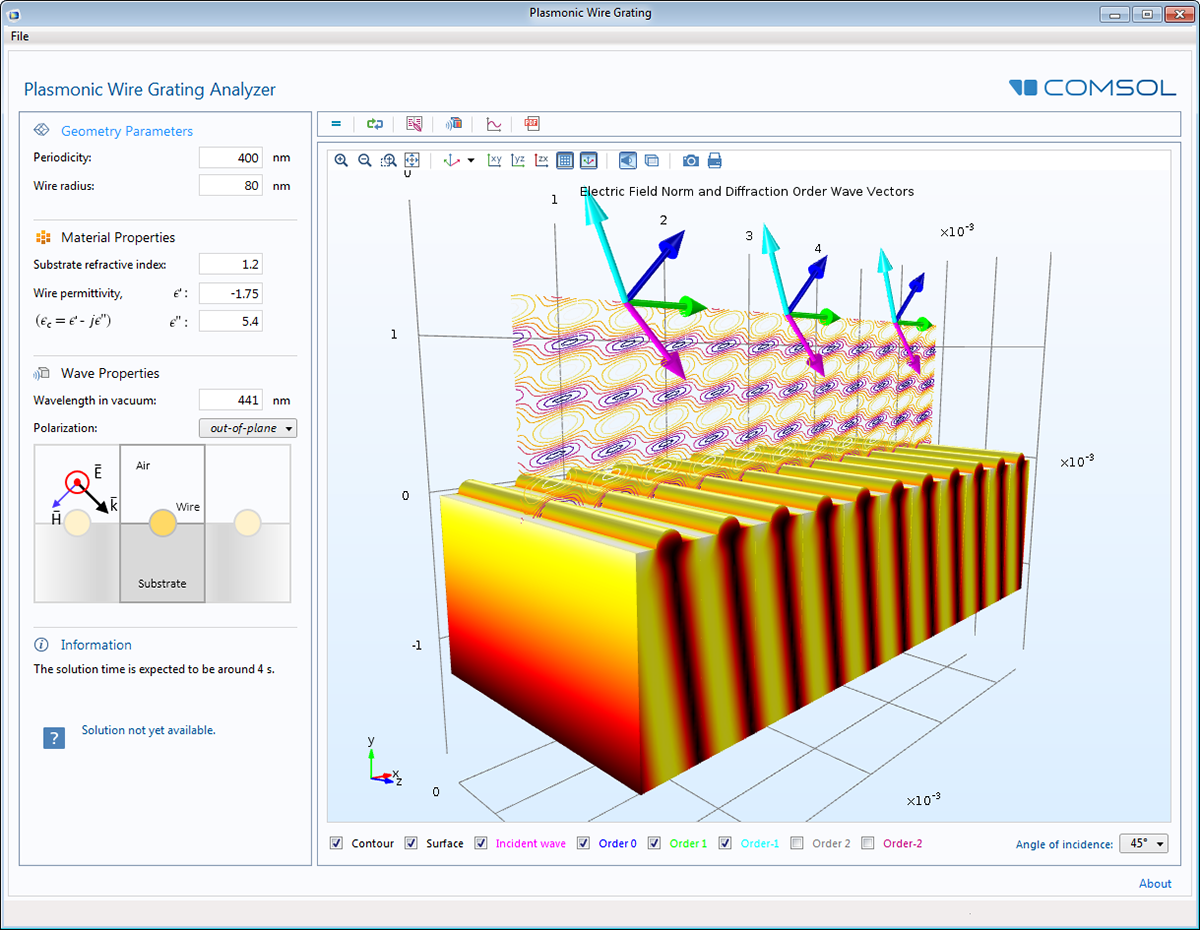
波动光学模块 Comsol 5 2a 发布亮点

高中物理第二章机械波第1 2节机械波的形成和传播波速与波长 频率的关系教学案教科版选修3 4 教科版高二选修3 4物理教学案下载 Word模板 爱问共享资料

万物都有波 通过一个公式可计算出任何物质的波长 包括你的波长 粒子 布罗意 棒球 网易订阅

最も人気のある 定在波波長 カービィ壁紙

峰值波长和光谱半波宽等红外led主要参数的介绍 电子发烧友网

中空型平板波导红外光谱仪的波长定标 中国光学期刊网

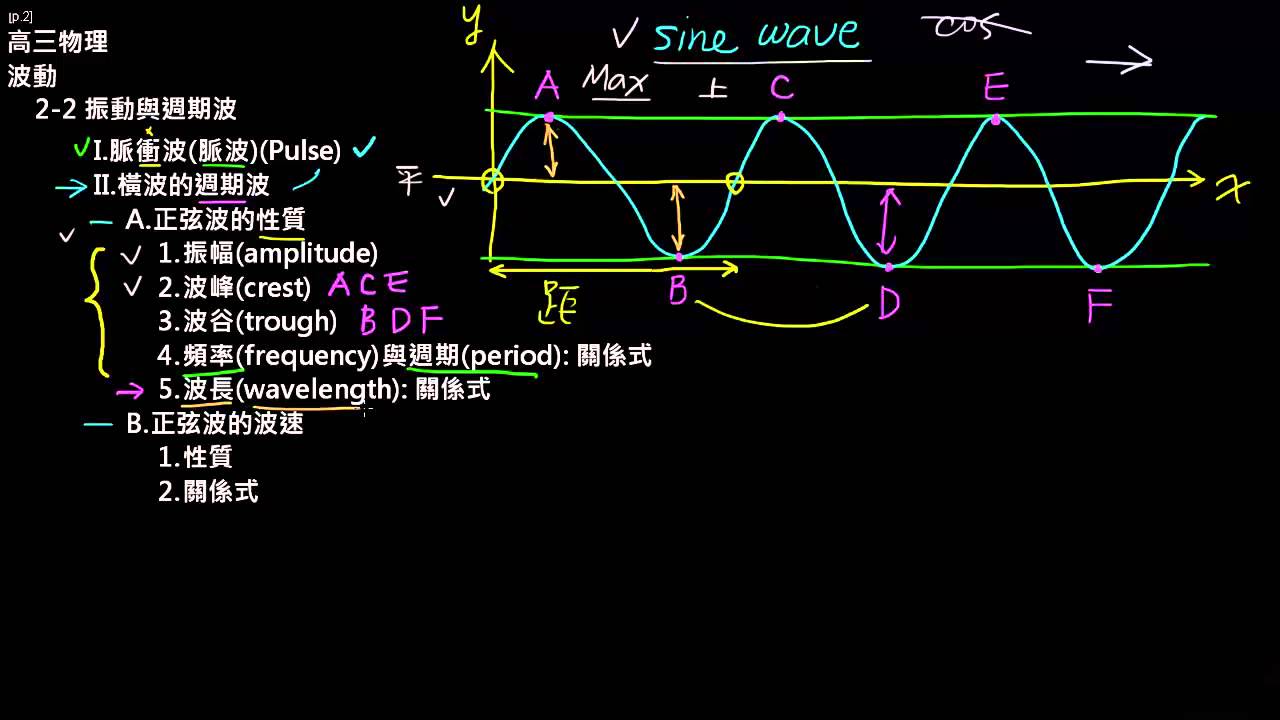
高三上物理2 2振動與週期波 4 正弦波性質總複習 波長波速關係式 Youtube

Physics Chapter 2 Wave 15

走进波分 10 Roadm 尚码园

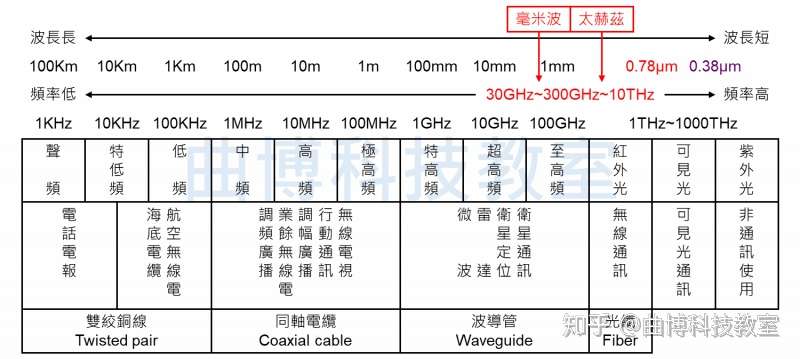
真正的6g来了 使用太赫兹电磁波频宽可达5g的100倍 知乎

发现当电磁波照射时 亚波长上的粒子 将入射能量耦合到振幅 腾讯新闻

定常波 わかりやすい高校物理の部屋

无线电波的波长 频率 与波段

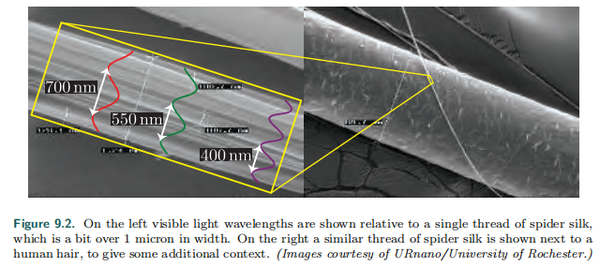
九 基于物理的着色 Physically Based Shading 知乎

1

Lms Ltsh Ilc Edu Tw Sys Read Attach Php Id

1

波動與聲音

最も人気のある 定在波波長 カービィ壁紙

小白系列 激光与激光器 知乎

频率与波长 频率波长61米 光的频率与波长的关系及单位

中空型平板波导红外光谱仪的波长定标 中国光学期刊网

噪声问题复杂化的因素 静噪基础教程 村田制作所

物联网lora系列 13 无线电磁波概述以及核心概念的澄清 速度 频率 周期 波长 幅度 功率 相位 干涉 文火冰糖 王文兵 的博客 程序员宅基地 程序员宅基地

怎么计算频率 最有妙招网

Rtshermjnh5cnm

4种方法来计算频率

怎么计算频率 最有妙招网

求解加詳解 Clear

1

駐波 维基百科 自由的百科全书

定常波 わかりやすい高校物理の部屋

怎么计算频率 最有妙招网

最も人気のある 定在波波長 カービィ壁紙

定常波 高校物理をあきらめる前に 高校物理をあきらめる前に

波動與聲音

不同元素是如何发光的 光的特性是什么 知乎

7224 72日大 有關波的性質 下列敘述中正確的是 Youtube

最も人気のある 定在波波長 カービィ壁紙

定常波 わかりやすい高校物理の部屋

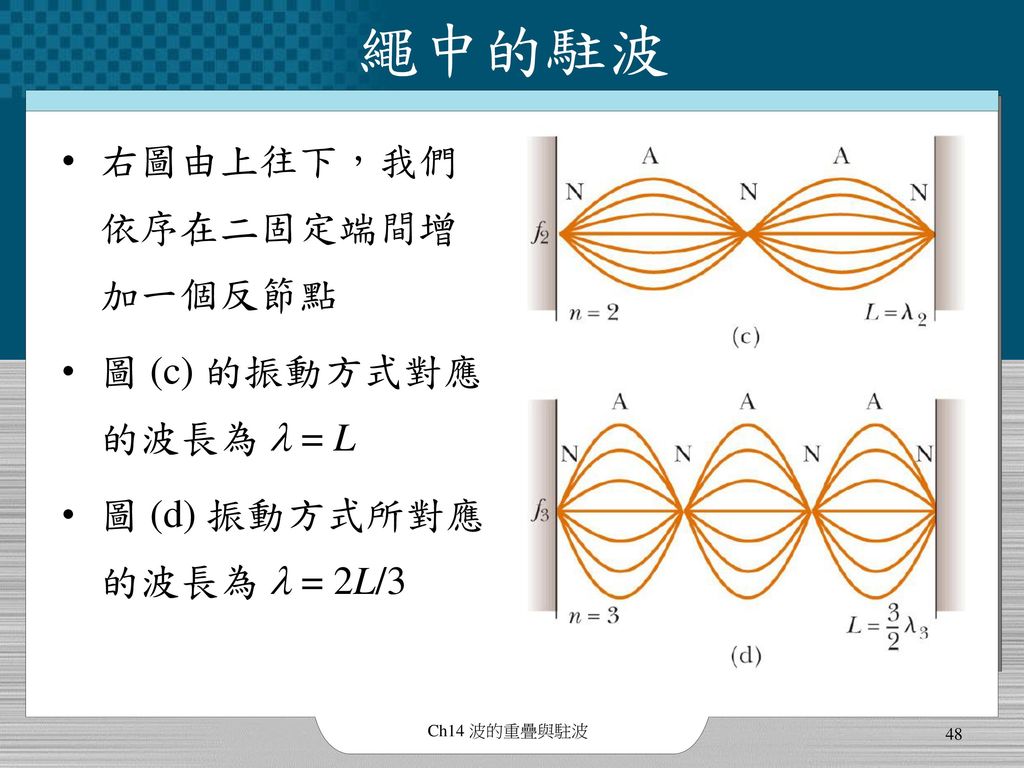
第十四章波的重疊與駐波 Ppt Download

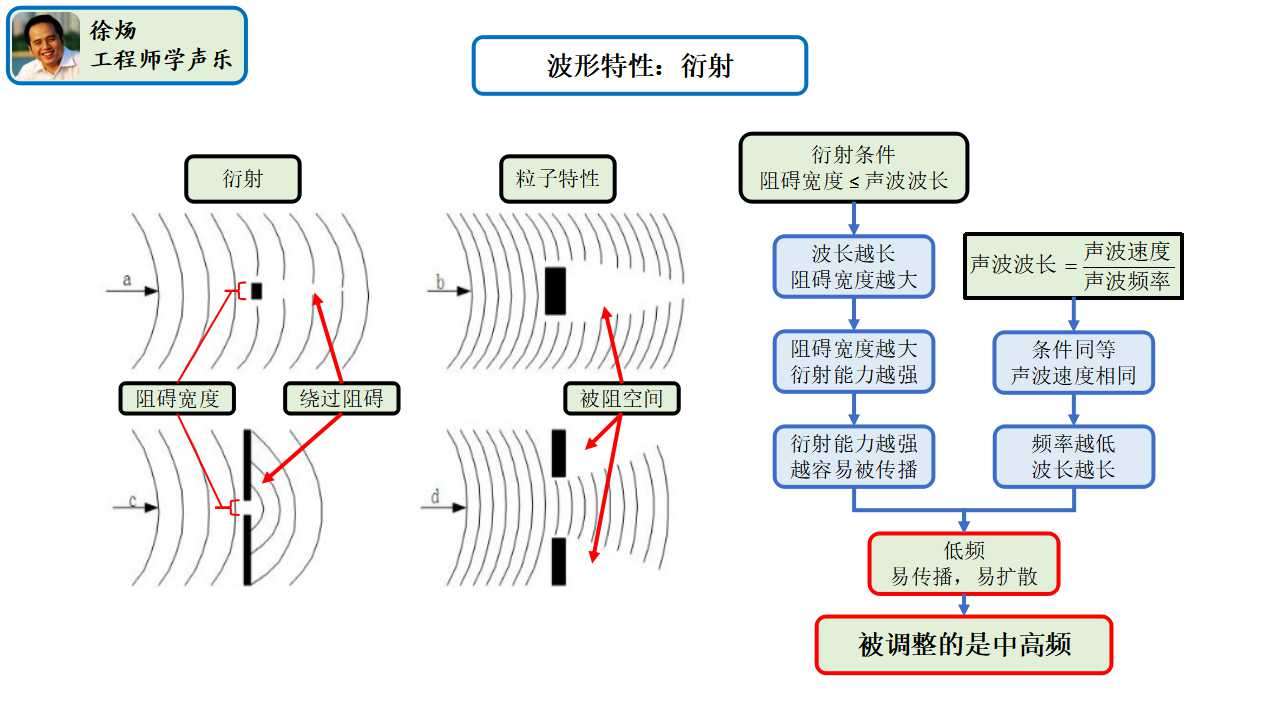
工程师学声乐07 波形特性 衍射 知乎

频率 维基百科 自由的百科全书

悟空问答 光子没有质量 请问光子有体积吗 烟泷寒水的回答 0赞

認識5g專題報導5 2 什麼是毫米波 Mmwave 與太赫茲 Thz Digitimes 智慧應用

电磁波的频率与波长的关系 Little Ox的博客 Csdn博客

Mm是什么单位

聲音頻率波長波動與聲音 Uhlwc

Rf射频 微波与毫米波频率与波长对照表 电磁

振幅和频率的关系

Lms Ltsh Ilc Edu Tw Sys Read Attach Php Id

定常波 わかりやすい高校物理の部屋

计算频率 提示 21

机械波及其图像 波特有的现象 高中物理知识点 高考圈

Incoming Term: 定在波 波長, 定在波 波長 半分, 定在波 波長 求め方, 定在波 反射 波長, 波長 定在波 定常波,